In this post, are shown the necessary concepts to make analysis of magnetic circuits, which is very similar to that of electric circuits.
Why analyze magnetic circuits?
The knowledge about analysis of this type of circuit is useful for design components that use magnetic field, as for exemple: relays, transformers, electric motors, generators, speakers, etc.
Magnetic field and magnetic permeability
Magnetic density flux (B) is defined by magnetic flux (\phi), in Wb (Weber), divided by area (A), in m^{2}.
B=\frac{\phi}{A}
The measurement unit for B is Wb/m^{2} or T (Tesla). The following equation is the relation between flux density and magnetizing force H, the latter is in Ae/m (ampère-turn per meter).
B=\mu H
Where \mu is the magnetic permeability. This is the product of vacuum’s magnetic permeability (\mu _{o}), a constant whose value is 4\pi \cdot 10^{-7}H/m, with relative permeability (\mu _{r}), which depends on material.
\mu =\mu _{o}\mu _{r}
Analogy with electric circuits
Reluctance
As shown in the post about resistance, capacitance, inductance, impedance and reactance, the material’s resistance is calculated using the formula:
R=\rho \frac{L}{A}
The materials have reluctance (\Re), which is a material resistance to magnetic flux, whose equation is:
\Re=\frac{l}{\mu A}
Where l is material’s length and A is cross section’s area. The reluctance is measured in rels or Ae/Wb (ampère-turn per weber).
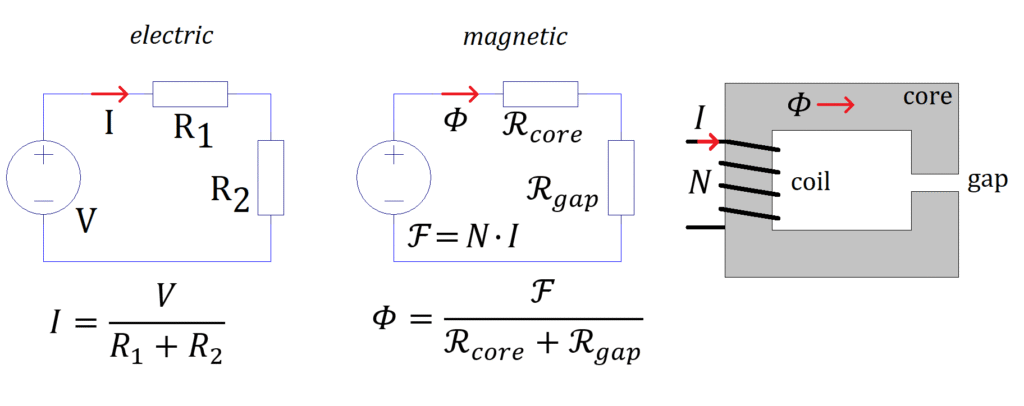
Ohm’s law for magnetic circuits
In a magnetic circuit, flux generators are coils, which produce the magnetomotive force (mmf) (\mathfrak{F}), in ampère-turn, that is coil’s current I multiplied by the number of turns N.
\mathfrak{F}=NI
The Ohm’s law equation for magnetic circuits.
\mathfrak{F}=\phi \cdot \Re

Ampère’s circuit law for magnetic circuits
Kirchhoff’s voltage law says that the sum of voltages and voltage drop in a closed loop circuit is zero. As shown in the post, whose link is below.
Circuit analysis (Part 1)Click here
Ampère’s circuit law claims that the algebraic sum of elevations and drops of magnetomotive force in a closed loop will always be zero.
\sum \mathfrak{F}=0
Magnetic flux
Just like in Kirchhoff’s current law, algebraic sum of fluxes entering in a node is equal to sum of fluxes going out of this node.
Air gap
It’s the air space between ferromagnetic materials. Since air’s relative magnetic permeability is only 1, the magnetizing force H and mmf are higher on air gap than on core.

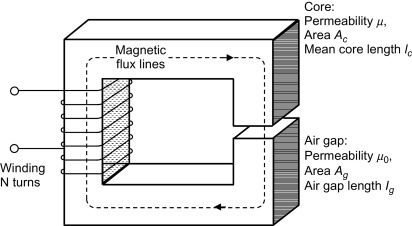
Obtaining the equation to the magnetic circuit above, using Ampère’s circuit law.
NI=H_{c}\cdot l_{c}+H_{g}\cdot l_{g}
- H_{c} and H_{g} are magnetizing forces of core and air gap, respectively.



