In this post is shown how to analyze a RC circuit, by that, with resistors and capacitors.
Charging phase
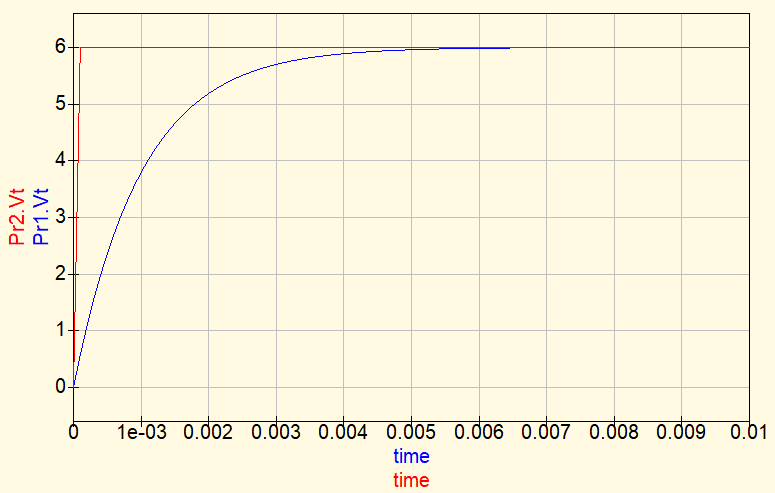
Let’s considerate the circuit below. In this simulator, I used a pulse generator with a long period to simulate a DC source with a switch which closes at instant t=0.

The capacitor does not allow voltage abrupt change, exists a transitional period of capacitor’s charging. During the charging phase, the voltage in capacitor follows this curve in blue in the following graphic. The source’s signal is in red.
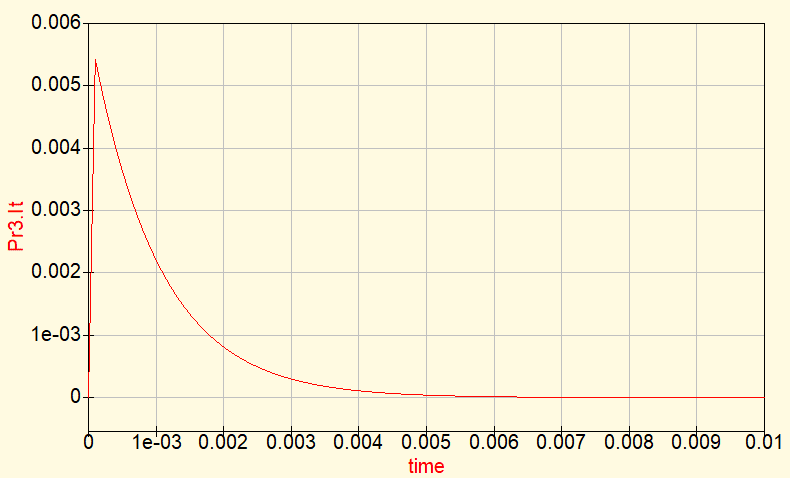
And this is the current’s graphic.
Voltage in capacitor follows this equation.
V_{C}(t)=V1(1-e^{\frac{-t}{\tau}})
- V_{C}(t) is the capacitor’s voltage in time function.
- V1 is the voltage of DC source.
- \tau is the time constant calculated in this form.
\tau=RC
The current in capacitor I_{C}(t) follows this equation.
I_{C}(t)=\frac{V1}{R}e^{\frac{-t}{\tau}}
Discharging phase
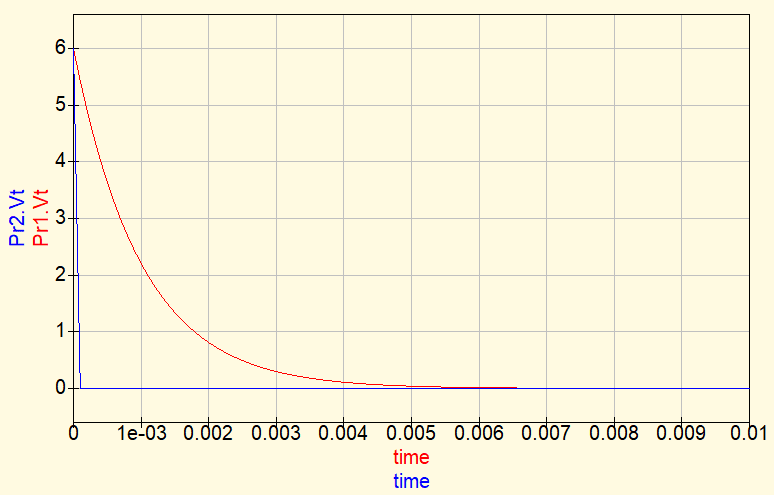
The pulse source in this circuit has been adjusted to start in 6 V and changes to 0 V. Simulating a switch opening in t=0.

The graphic of capacitor’s discharging voltage in red.
The discharging current of capacitor in graphic and its formula respectively.

I_{C}=-\frac{V1}{R}e^{\frac{-t}{\tau }}
Initial values
In some situation of RC circuit analysis, the capacitor already has some charge. In this case, must use the equation below. V_{i} is the initial voltage before charging and V_{f} is the final voltage after charging.
V_{C}(t)=V_{f}+(V_{i}-V_{f})e^{\frac{-t}{\tau}}
If V_{i} is equal to zero, stays equal to capacitor’s charging equation.
V_{C}(t)=V_{f}+(0-V_{f})e^{\frac{-t}{\tau}}
V_{C}(t)=V_{f}(1-e^{\frac{-t}{\tau}})
Voltage’s curve in graphic, here the capacitor has some initial voltage. In this case starts in 2 V.

The graphic of current is the same of without initial charge case, to calculate peak current I_{p}.
I_{p}=\frac{V1-V_{C}}{R}
Instant values
How to determine voltage or current in a capacitor in a determined instant of time? Making demonstration to obtain the formula.
V_{C}=V_{f}+(V_{i}-V_{f})e^{\frac{-t}{\tau}}
V_{C}-V_{f}=(V_{i}-V_{f})e^{\frac{-t}{\tau}}
\frac{1}{e^{\frac{-t}{\tau}}}=\frac{V_{i}-V_{f}}{V_{C}-V_{f}}
e^\frac{t}{\tau}=\frac{V_{i}-V_{f}}{V_{C}-V_{f}}
Applying neperian logarithm in both sides.
ln(e^{\frac{t}{\tau}})=ln(\frac{V_{i}-V_{f}}{V_{C}-V_{f}})
\frac{t}{\tau}=ln(\frac{V_{i}-V{f}}{V_{C}-V_{f}})
This is the equation to calculate time instant in a value V_{C}.
t=\tau ln(\frac{V_{i}-V{f}}{V_{C}-V_{f}})



