This post’s subject is carbon 14. A radioactive isotope which allows determining the age of an artifact or living being from thousand of years ago.
Carbon 14 formation
Carbon 14 is a carbon’s radioactive isotope with 6 protons, 6 electrons, and 8 neutrons.
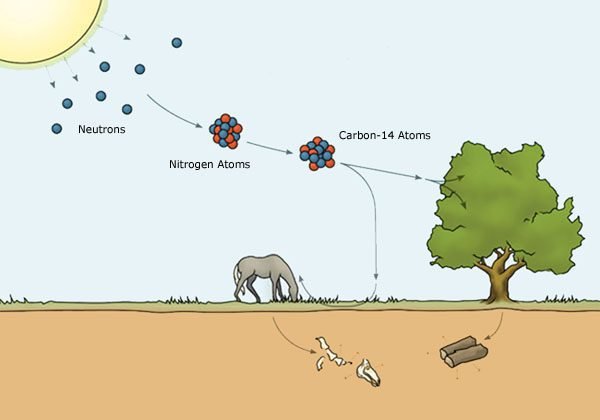
Cosmic rays that arrives in the upper atmosphere produce neutrons, the later collide with nitrogen 14, producing carbon 14.

The carbon 14 (C14) combines with oxygen gas to form carbon dioxide (CO_{2}), which is absorbed by plants. The latter are consumed by animals, which consequently absorb the isotope when they feed themselves.
When an animal or plant dies, doesn’t absorb C14 anymore. This isotope decays in nitrogen 14.
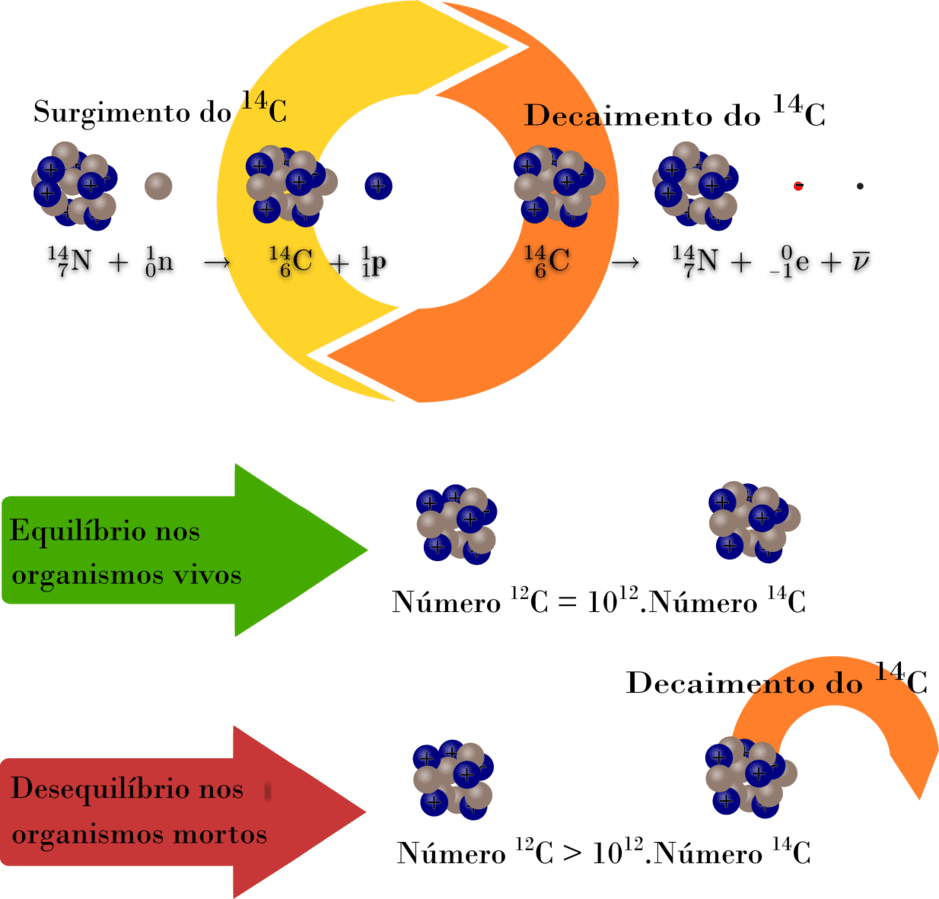
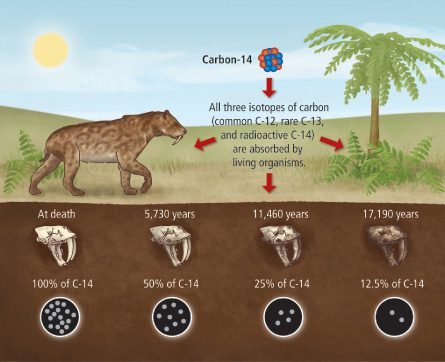
When older the organic material, less the quantity of reminiscent carbon 14 and lower the emission of beta particles (electrons).
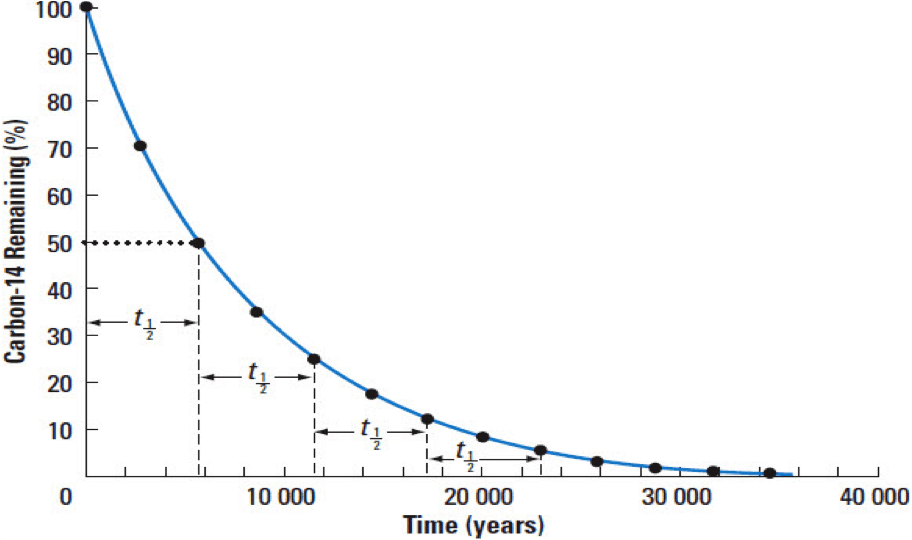
Radioactive decay calculation
The decay curve follows the equation below.
R=R_{0}e^{-\lambda t}
- R_{0} is the decay rate when t=0, by that, in the moment of organism’s death, in decay/seconds or becquerel (Bq).
- R is the current decay rate.
- \lambda is the disintegration constant, whose value is:
\lambda=\frac{ln2}{T_{1/2}}=\frac{ln2}{5730}=1,209\cdot 10^{-4}
- t is the time passed since the organism died.
- T_{1/2} is the isotope’s half-life.
The formula to calculate t is just a manipulation of previous equation.
t=\frac{-ln(\frac{R}{R_{0}})}{-ln2}\cdot T_{1/2}
The equations shown serve to all radioactive isotopes and elements.
Errors in measurement
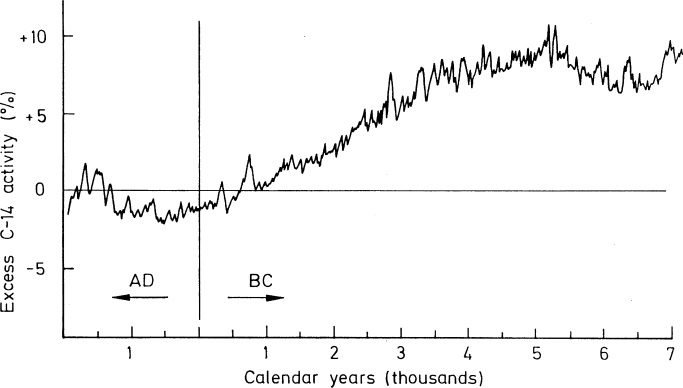
Dating by carbon 14 is only reliable for samples until 50,000 years ago. The quantity produced in the atmosphere isn’t constant, which might cause errors in measurements.
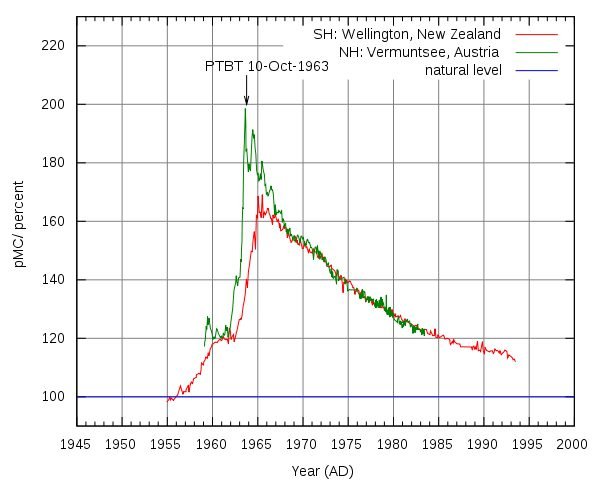
There was an increase in concentration of this isotope due to nuclear tests in the last century. Generating a peak in the 1960s.
The living beings have many other radioactive isotopes, for example, the potassium 40, whose half-life is 1.248 billion years, In the next part, I will explain the methods used to measure C14 decay.



