In this post, will be explained the cyclone’s formation. Cyclones have different names depending on the world’s region. Hurricane in the Americas and typhoon in Asia.
Formation of cyclones
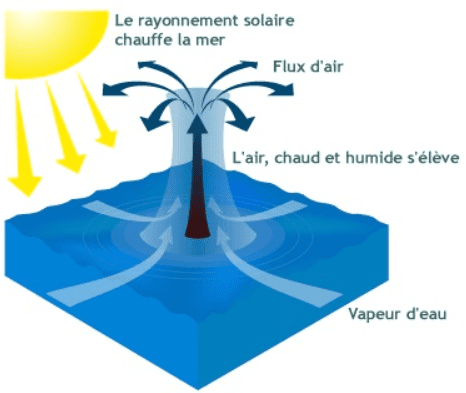
Are formed in the oceans, where atmospheric pressure is low, the temperature is above 26ºC and humidity above 70%. The ocean’s water is evaporated and enters in contact with cold air mass.
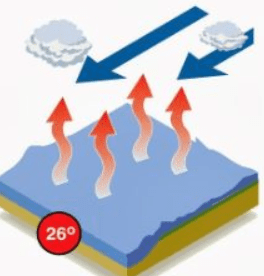
The hot air cools down when rises in the atmosphere and goes down for being denser. The steam goes up to get cooler and form clouds.
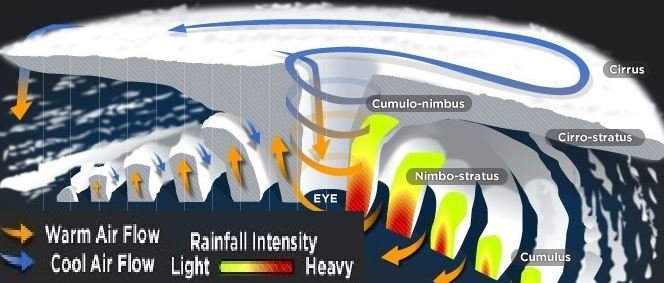
A low-pressure column is created and hot air winds are formed and climb in the low-pressure column, while the cold air goes down through the middle of the column. The Coriolis effect makes the winds move in a spiral.

The humidity and water evaporation feed the hurricane, the wind speed increases and convective cells are formed.
Cyclones lost power when reaching the continent because it is no longer fed by evaporation and humidity. Due to Coriolis force, the cyclones in the North hemisphere spin in anticlockwise, while in the southern hemisphere, spin in clockwise. Only can be formed from 5º of latitude because this force is null in the Equator.


The cyclone’s “eye” is much calmer, has the wind in a maximum of 30 km/h. That’s because winds move in circles and the speed is concentrated outside the “eye”. The cyclone can last many days and has many kilometers of extension.
Coriolis force
What is the Coriolis force? It is an inertial force caused by Earth’s rotation which is caused by the deflection of an object’s trajectory. The black sphere moved in a straight line, but in relation to the orange point, the sphere made a curve.

Why is this force null in the Equator? Below there is the equation that calculates the Coriolis force vector \vec{F}.
\vec{F}=-2m\cdot (\vec{v}\times \vec{\omega})
\vec{v} is the object’s speed vector, m is the object’s mass and \vec{\omega} is the Earth’s angular rotation speed vector parallel to it’s polar axis.
In the equator, \vec{v} is parallel to \vec{\omega}. So, the vector product (\times) is zero when the wind moves to the north or south direction. Below is another form of the equation.
f=\frac{F}{m}=2v\omega sen\theta
\theta is the latitude’s angle. In the equator, \theta is zero, so the force is null.Classification
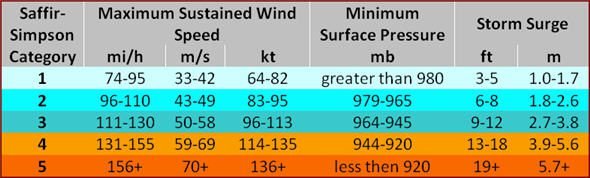
Cyclones are classified by the Saffir-Simpson scale, it considers speed, pressure, and increase of sea level (Storm Surge).