Meeting requests, the subject is about basic concepts of AC. Has been already mentioned AC in the post about electromagnetism, this post will go deeper.
To see basic concepts of electromagnetism, click in the button below.
Wave properties
What is frequency? Is the number of cycles per second in Hertz (Hz), this cycle can be the swinging of a pendulum, the intensity and direction change of an electrical current, the number of turns an object travels in circular trajectory, the amplitude variation of a sound wave, etc.
1 Hz = 1 cycle per second
The period T simply is the necessary time to complete a cycle and the inverse of frequency.
T=\frac{1}{f}
Every wave has amplitude, which is the distance between the peak or valley and the wave’s “zero” point.

A wave length (\lambda) is the distance between two peaks or valleys.

This is the formula to calculate the wave length, v is the speed.
\lambda=\frac{v}{f}
This is the angular speed formula in radians per second (rad/s).
\omega =2\pi f
Other definitions
- Instant value: Is the amplitude value in a determined time.
- Peak-to-peak value (V_{p-p}): Is the sum of positive and negative amplitudes. In the example below, the peak-to-peak voltage of a wave with 10 V amplitude is 20 V.

- Effective or RMS value (V_{rms}): Is the voltage or current value equivalent to DC value. An alternate signal with effective value of 10 V provides the same power to a resistance if were a 10 V DC signal. The effective value of a voltage or current is equal to 0.707 of maximum value V_{m} or I_{m}.
I_{rms}=\frac{I_{m}}{\sqrt{2}} or V_{rms}=\frac{V_{m}}{\sqrt{2}}

The demonstration involves use a trigonometric identity and match average AC power with DC power.
- Average value: It is calculated dividing the area around the curve by the period. A wave with positive and negative areas equal in a complete period has average value zero.

To calculate the average value of a sinusoid semicircle, we have to use integrals which get the result below.
V_{av}=\frac{2}{\pi }V_{m}=0,637V_{m}

Description of AC sinusoidal wave
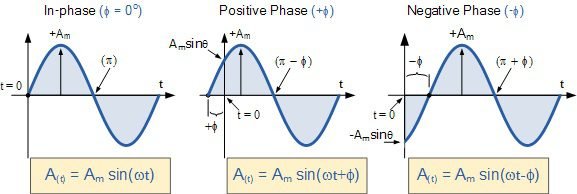
An AC sinusoidal wave is represented by this equation. t is the time.
V(t)=V_{m}sen(2\pi ft+\phi )
\phi is the phase angle in degree or radians, represents the wave position in relation to initial time. If the wave starts in t=0, then \phi is equal to zero. If the wave starts before t=0, it is advanced and \phi is positive. If starts after t=0, it is delayed and \phi is negative.
Pure inductors in AC has the voltage 90º or \frac{\pi }{2} advanced in relation to current.

Pure capacitors in AC has the current 90º or \frac{\pi }{2} advanced in relation to voltage.

A cossinusoid is a 90º advanced curve in relation to sinusoid.

The phasor diagram is another way to represent a sinusoid. The curve is represented by a vector called phasor, which turns anticlockwise in \omega speed. The phase angle represents the angle the phasor forms in relation to horizontal axis.

This is the phasor form to represent an AC voltage or current.
V=V_{rms}\angle \phi



