This post’s subject is degrees of freedom (DOF). The concept in mechanics and how to calculate DOF in a mechanical system.
Definition in mechanics
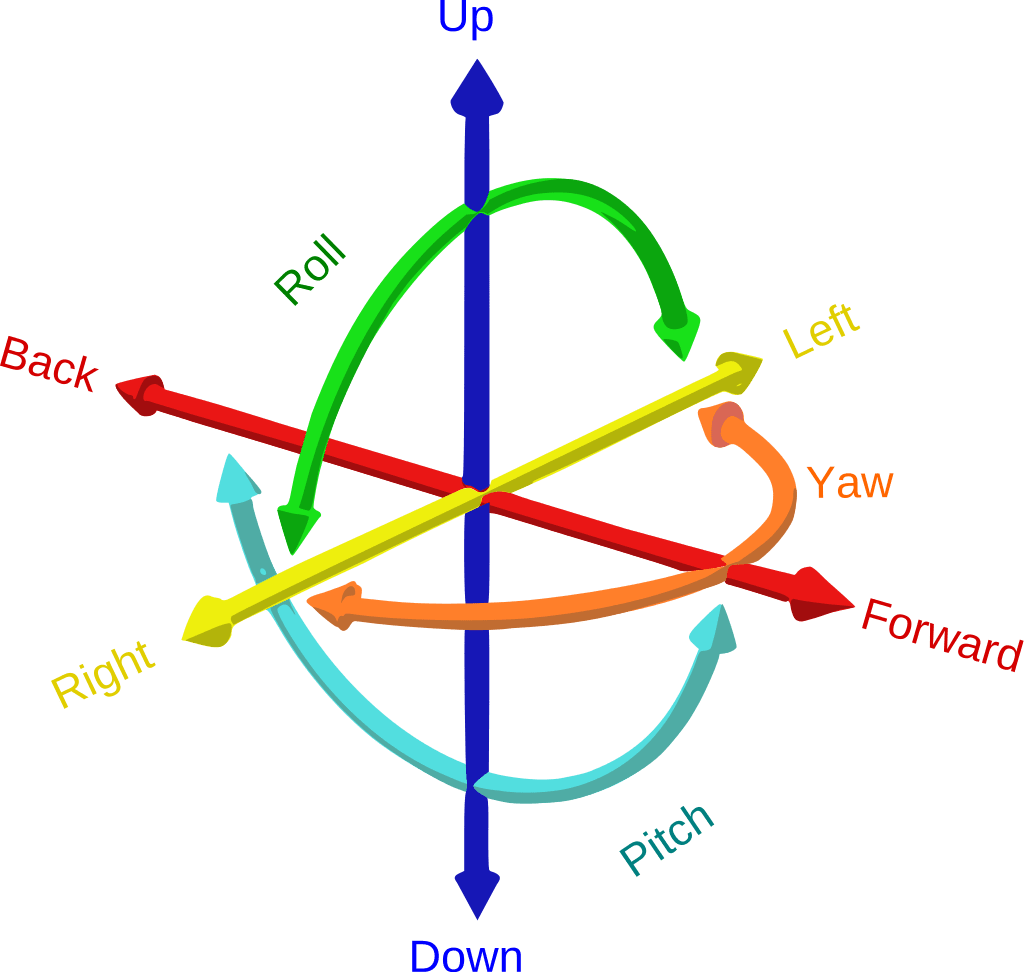
Degrees of freedom are the number of variables that indicates a mechanism’s position. Each axis of coordinates x, y, and z is a translation degree of freedom.
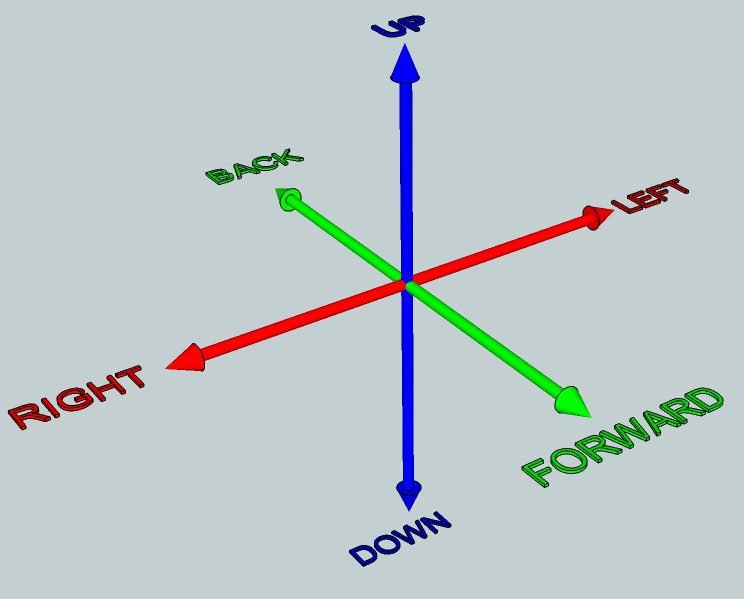
And each rotational motion perpendicular to one of the axis is a rotational degree of freedom.
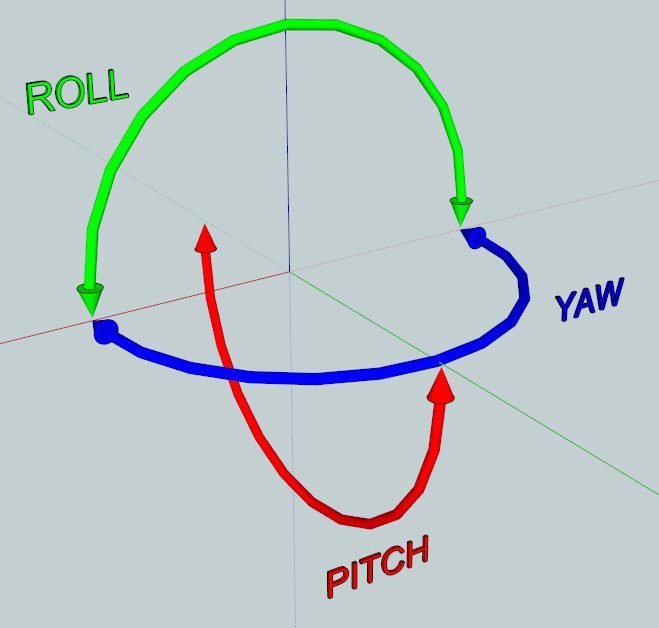
Therefore, a body that moves in a three-dimensional space has 6 degrees of freedom.
The figure below shows multiple systems of object pairs and its degrees of freedom (DOF) between parenthesis.
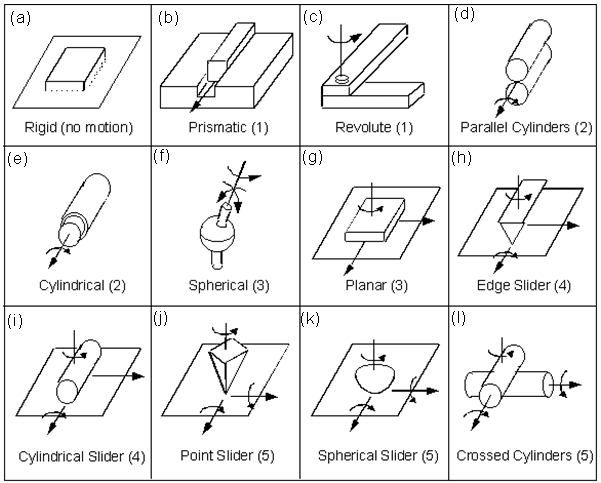
Is it possible for a mechanical system to have more than 6 DOF? The answer is yes, human arm has 7.
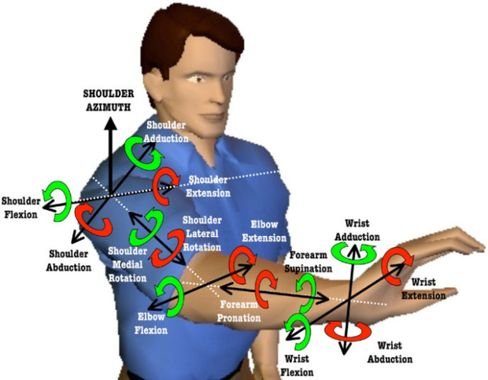
This humanoid robot has 9 DOF.

Determining degrees of freedom
How about more complex mechanical systems? How to calculate the number of necessary actuators for mechanisms like this?
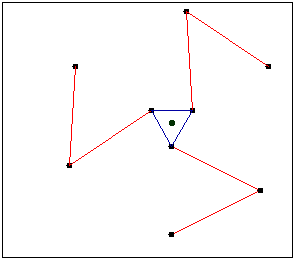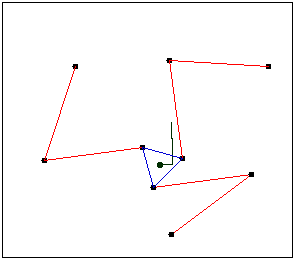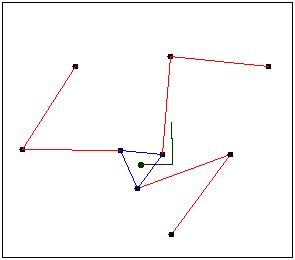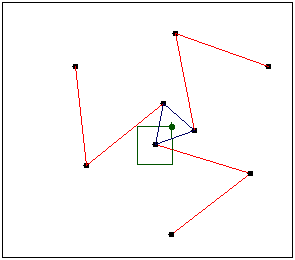
Grübler equation
This is the equation to calculate mobility.
DOF=m(N-1)-\sum_{i=1}^{J}(m-f_{i})
- N: Number of links, A link is a part which can connect to two or more parts. Also can be the surface or carcass.
- J: Number of pair or joints, which connects two links.
- m: Mobility of a body. As shown before, 6 in a three-dimensional space and 3 in a plane.
- f_{i}: Number of degrees of freedom in pair i.
Using this system as example. Have 4 links N=4 and 4 joints J=4. m=3 because it’s in a plane.
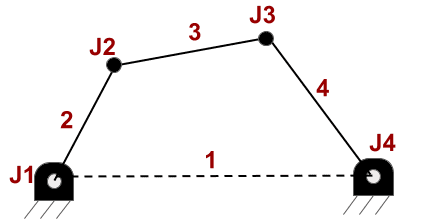
Two bodies separated in plane have DOF=6. When these bodies are linked by a joint, they lose 2 and get DOF=4, therefore f_{i}=1. Calculating mobility.
DOF=3(4-1)-\sum_{i=1}^{4}(3-1)
DOF=3(4-1)-4\cdot (2)=9-8=1
How many DOF have this machine with a double joint and a slider? N=8 and m=3.
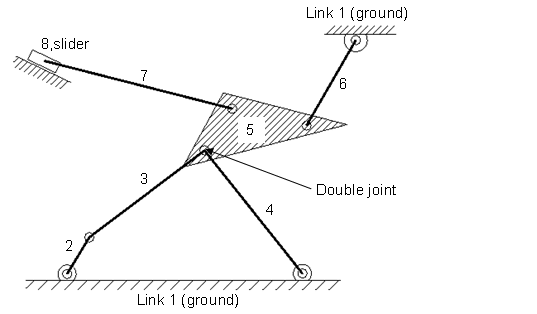
The double joint count as 2, therefore J=10 and all pairs have 1 mobility degree f_{i}=1.
DOF=3(8-1)-\sum_{i=1}^{10}(3-1)
DOF=24-3-2\cdot 10=1
And this one with a wheel? m=3 and N=4.
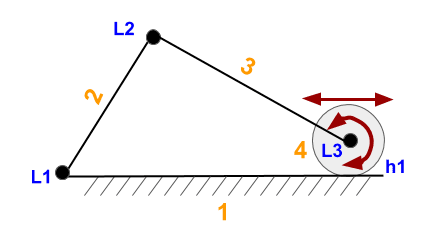
The pair wheel-surface has 2 degrees of freedom, by that, f_{4}=2. Therefore, equation is:
DOF=3(4-1)-[(3-1)+(3-1)+(3-1)+(3-2)]
DOF=12-3-[3(3-1)+(3-2)]=9-3\cdot 2-1=2
How many degrees of freedom there are in the mechanism showed before? m=3, N=8 (including surface), J=9 e f_{i}=1.
[WPGP gif_id=”19460″ width=”600″]
DOF=3(8-1)-\sum_{i=1}^{9}(3-1)
DOF=24-3-9\cdot 2=24-3-18=3
To apply for three-dimensional systems, considerate m=6 and count DOF of all pairs. This Grübler equation can be simplified for two dimensions.
DOF=3(N-1)-2J_{1}-J_{2}
- J_{1}: joints with 1 DOF.
- J_{2}: joints with 2 DOF.
And for three dimensions.
DOF=6(N-1)-5J_{1}-4J_{2}-3J_{3}-2J_{4}-J_{5}
These simplifications are called Kutzbach equation. The number of necessary actuators to activate a mechanism is equal to degrees of freedom.
Degrees of freedom lower or equal than zero
When the degree of freedom or mobility is equal to zero, it means that is a structure and not a mechanism. If it is lower than 0, the structure is preloaded and has a force accumulation which generates mechanical tensions.



