O que são graus de liberdade?

O assunto deste post são os graus de liberdade (DOF). O conceito na mecânica e como calcular DOF em um sistema mecânico.

Definição na mecânica

Graus de liberdade ou mobilidade são o número de variáveis que indicam a posição de um mecanismo. Cada eixo das coordenadas x, y e z é um grau de liberdade de translação.

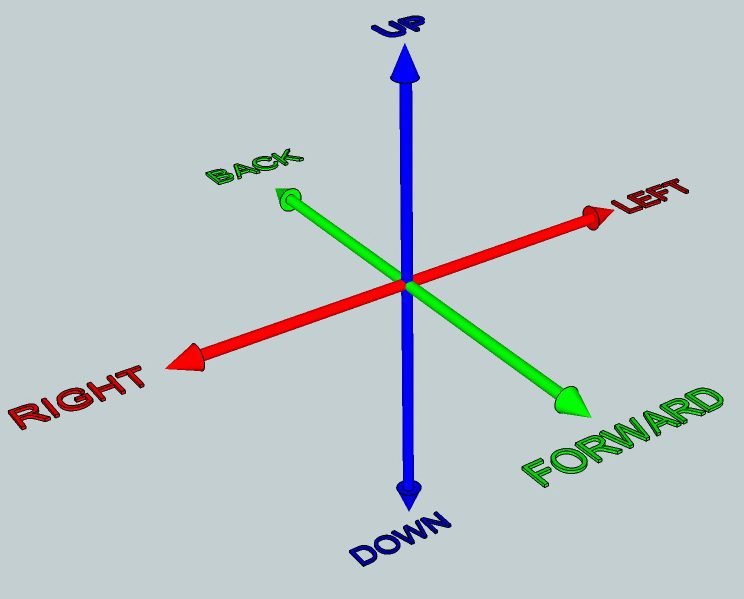
E cada movimento de rotação perpendicular a um dos eixos é um grau de liberdade rotacional.

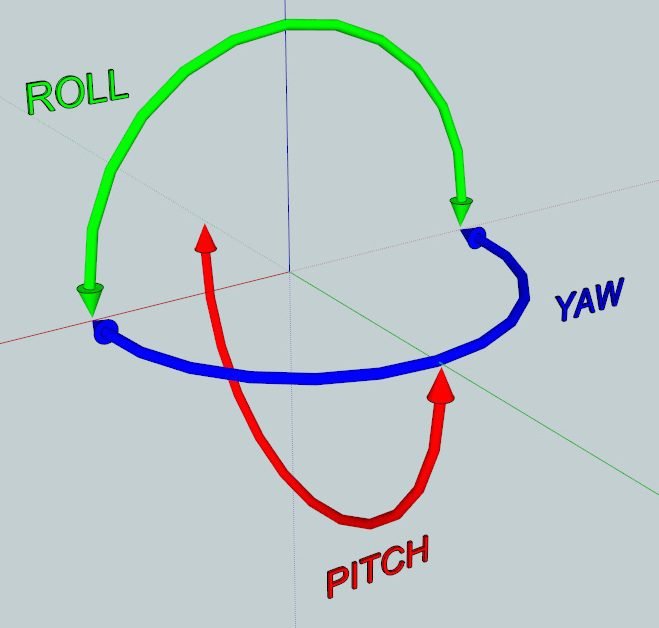
Portanto, um corpo que se movimenta em um espaço tridimensional tem no total 6 graus de liberdade.

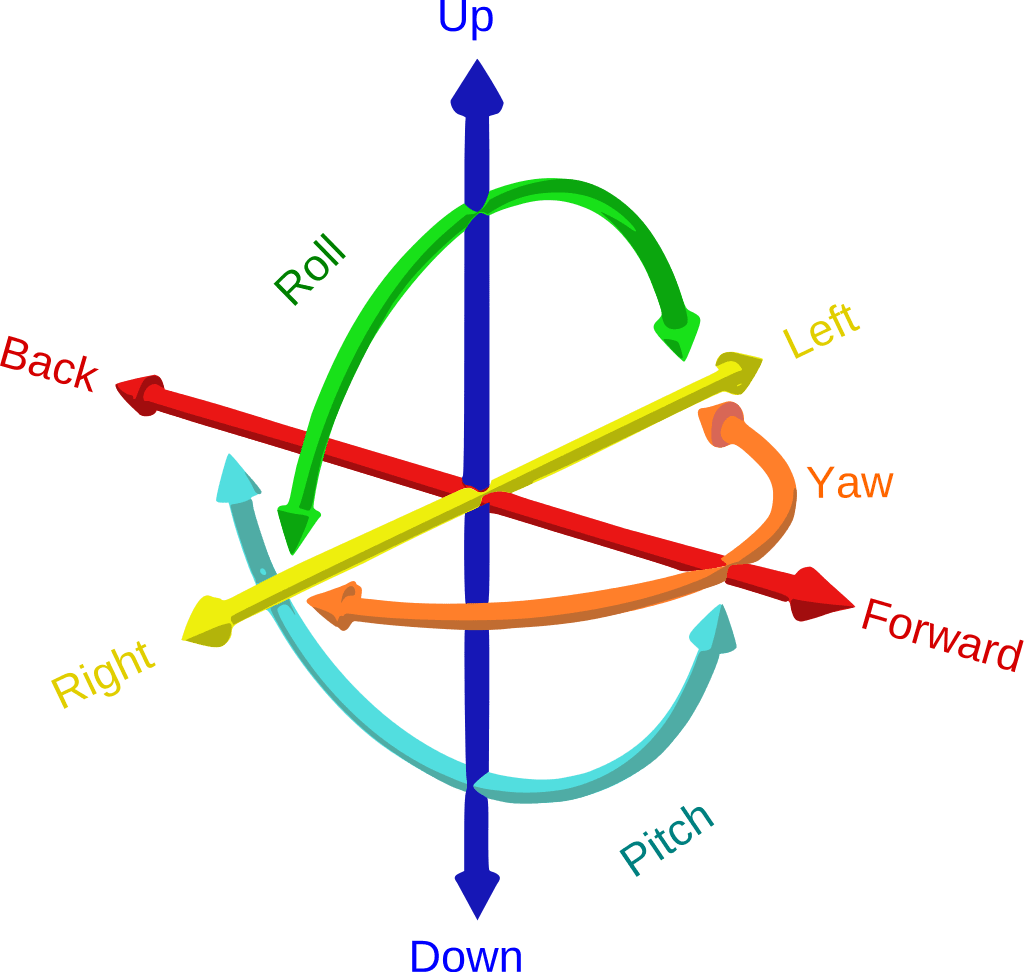
A figura abaixo mostra vários sistemas de pares de objetos e seus graus de liberdade (DOF) entre parênteses.

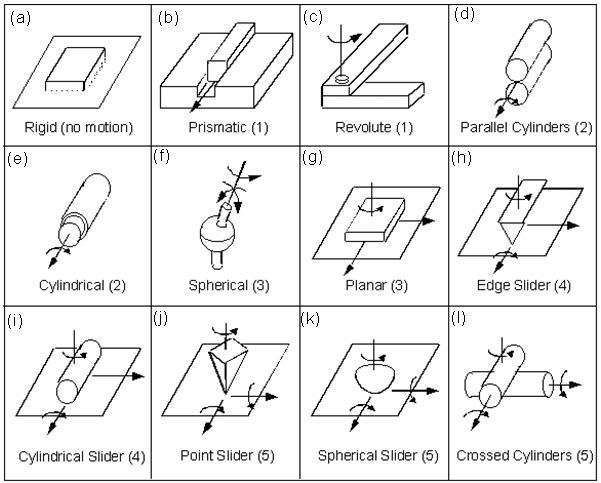
É possível um sistema mecânico ter mais de 6 DOF? A resposta é sim, o braço humano tem 7.

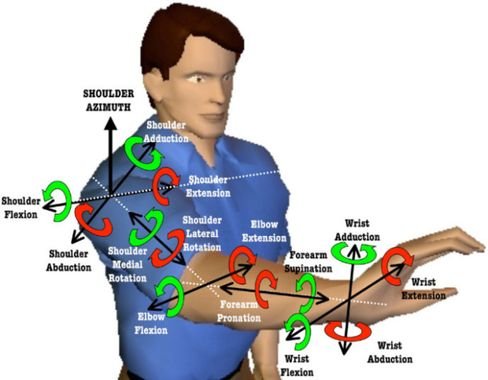
Este robô humanoide possui 9 DOF.

Determinando graus de liberdade

E sistemas mecânicos mais complexos? Como calcular o número de atuadores necessários para mecanismos como este?

Equação de Grübler

Esta é a equação para calcular a mobilidade.

DOF=m(N-1)-\sum_{i=1}^{J}(m-f_{i})

• N: O número de elos. Um elo é uma peça que pode se conectar com outras peças. Pode ser a superfície ou carcaça.
• J: O número de pares ou juntas, que ligam dois elos.
• m: A mobilidade de um corpo. Conforme mostrado anteriormente, 6 em um espaço tridimensional e 3 em um plano.
• f_{i}: O número de graus de liberdade no par i.

Usando este sistema como exemplo. Tem 4 elos N=4 e 4 juntas J=4. m=3 pois está em um plano.

Dois corpos separados no plano possuem DOF=6. Quando estes corpos estão ligados por uma junta, perdem 2 e ficam com DOF=4, portanto f_{i}=1. Calculando a mobilidade.

DOF=3(4-1)-\sum_{i=1}^{4}(3-1)

DOF=3(4-1)-4\cdot (2)=9-8=1

Quantos DOF tem esta máquina com uma junta dupla e uma barra deslizante? N=8 e m=3.

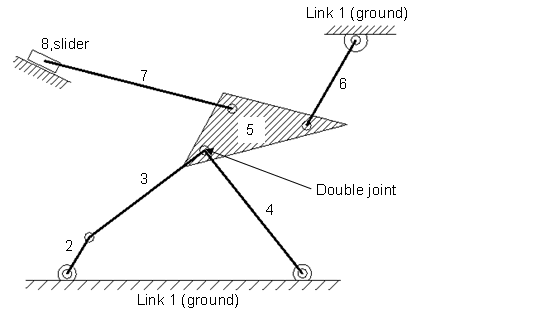
Uma junta dupla conta como 2, logo J=10 e todos os pares contêm 1 grau de mobilidade f_{i}=1.

DOF=3(8-1)-\sum_{i=1}^{10}(3-1)

DOF=24-3-2\cdot 10=1

E este aqui com uma roda? m=3 e N=4.

O par roda-superfície tem dois graus de liberdade, ou seja, f_{4}=2. Portanto, a equação fica:

DOF=3(4-1)-[(3-1)+(3-1)+(3-1)+(3-2)]

DOF=12-3-[3(3-1)+(3-2)]=9-3\cdot 2-1=2

Quantos graus de liberdade há no mecanismo mostrado anteriormente? m=3, N=8 (incluindo a superfície), J=9 e f_{i}=1.

[WPGP gif_id=”19424″ width=”600″]

DOF=3(8-1)-\sum_{i=1}^{9}(3-1)

DOF=24-3-9\cdot 2=24-3-18=3

Para aplicar a sistemas de três dimensões, considere m=6 e conte o DOF de todos os pares. Esta equação de Grübler pode ser simplificada para 2 dimensões.

DOF=3(N-1)-2J_{1}-J_{2}

• J_{1}: juntas com 1 DOF.
• J_{2}: juntas com 2 DOF.

E para 3 dimensões.

DOF=6(N-1)-5J_{1}-4J_{2}-3J_{3}-2J_{4}-J_{5}

Estas simplificações são chamadas de equações de Kutzbach. O número de atuadores necessários para acionar um mecanismo é igual ao número de graus de liberdade.

Graus de liberdade menor ou igual a zero

Quando o grau de liberdade ou mobilidade é igual a zero, quer dizer que é uma estrutura e não um mecanismo. Se for menor que 0, a estrutura está pré-carregada e tem um acúmulo de forças que geram uma tensão mecânica.