The cyclotron is a particle accelerator invented in 1932, for research in High Energy Physics and isotope production.
Cyclotron operation principle
It was built by the American physicist Ernest Lawrence, with his student M. Stanley Livingston. Consist of two half cylinders of hollow conductors in a “D” shape, connected to a high frequency alternate voltage source. The conductors are in a vacuum chamber and receive a perpendicular and uniform magnetic flux density (\vec{B}).
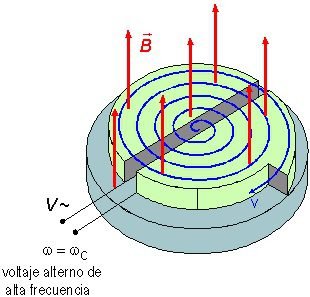
The cyclotron needs an ion source, which is above or below ‘D’ conductors. This source is an ionized gas by high voltage, called plasma, or a solid ionized by arc flash. Ions are launched to cyclotron’s center, between the conductors, and accelerated by electric and magnetic fields. Between the ‘Ds’, there is an electric field with \vec{E} intensity, which exerts an electric force (\vec{F}) over the particle with q, this force’s equation is:
\vec{F}=q\cdot\vec{E}
Due to this force, the particle with mass m receives an acceleration \vec{a} and gains speed. Using the Newton’s second law.
\vec{F}=q\cdot\vec{E}=m\cdot\vec{a}
\vec{a}=\frac{q\cdot\vec{E}}{m}
The potential difference (\Delta V) of an uniform electric field (\vec{E}) is:
\Delta V=\vec{E}\cdot d
Where d is the distance between conductors. Therefore, particle’s acceleration on cyclotron is:
\vec{a}=\frac{q\Delta V}{md}
The equation shows that higher the potential difference, or voltage, between ‘Ds’ and lower the distance between them, higher is particle’s acceleration. When a particle enters on conductor’s cavity, it enters a region with a magnetic field perpendicular to the electric field, consequently, the particle receives a force perpendicular to speed vector, its called Lorentz force.
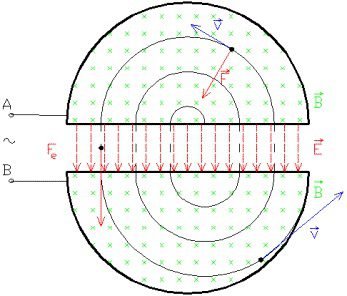
Lorentz force
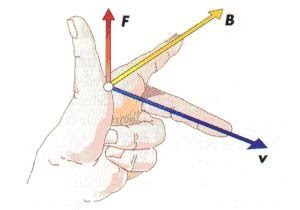
If the charge is negative, just change the force to opposite direction. Lorentz force (\vec{F}) equation is:
\vec{F}=q\vec{v}\times\vec{B}
Where,
- \vec{v} is particle’s velocity vector.
\times isn’t the same multiplication well known by everyone. This symbol is the vectorial product, used between vectors. In cyclotron’s case, Lorentz force equation can be simplified in this way.
F=qvBsen90^{\circ}
Newton’s second law applied to uniform circular motion.
F=m\frac{v^{2}}{R}
Equaling the two forces.
qvB=m\frac{v^{2}}{R}
R=\frac{mv}{qB}
When a particle is between ‘Ds’, it’s accelerated by electric field, gaining more speed. As the equation above shows, higher the speed, higher the trajectory’s radius. That’s why the particle makes bigger turns inside the cyclotron, until obtains sufficiently high speed to get out of ‘Ds’ region and hit a target.
Resonance frequency
Considering the angular speed (\omega).
\omega=\frac{v}{R}
qvB=m\frac{v^{2}}{R}
v=\frac{qBR}{m}
\omega=\frac{qB}{m}
With the particle’s angular speed, you can calculate resonance frequency (f) of cyclotron.
f=\frac{\omega}{2\pi}=\frac{qB}{2\pi m}
The oscillator that supplies ‘D’ conductors must operate at the same frequency of resonance frequency. So that the particle receives an electric force as soon as enters the electric field region between conductors. When the particle reaches speeds closer to the light, change on body’s mass must be considered.
m=\frac{m_{o}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}
m_{o} is original mass, c is the speed of light in vacuum, and m is body’s mass when reaches close to light speeds. Therefore, resonance frequency becomes.f=\frac{qB}{2\pi m_{o}}\sqrt{1-\frac{v^{2}}{c^{2}}}
Current applications of cyclotron
- Produce isotopes to use in a Positron Emission Tomography (PET).
- Production of isotopes to synthesize radiopharmaceuticals for cancer treatment.

- Cyclotrons are still used in nuclear physics experiments, to transmute atomic nuclei or bombard them.



