O assunto deste post é o giroscópio. Um instrumento de grande utilidade para os aparelhos eletrônicos e para as navegações aérea, marítima e espacial.
Princípio de funcionamento
Momento angular
Todo objeto em rotação tem um momento angular paralelo ao eixo de rotação.
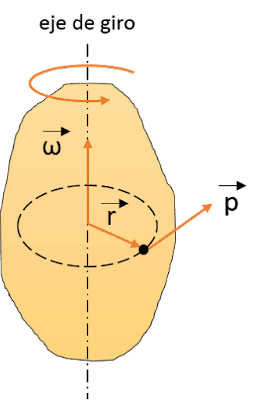
A fórmula para calcular o vetor momento angular \vec{L} de um sólido rígido, em kg\cdot m^{2}/s.
\vec{L}=I\cdot \vec{\omega}
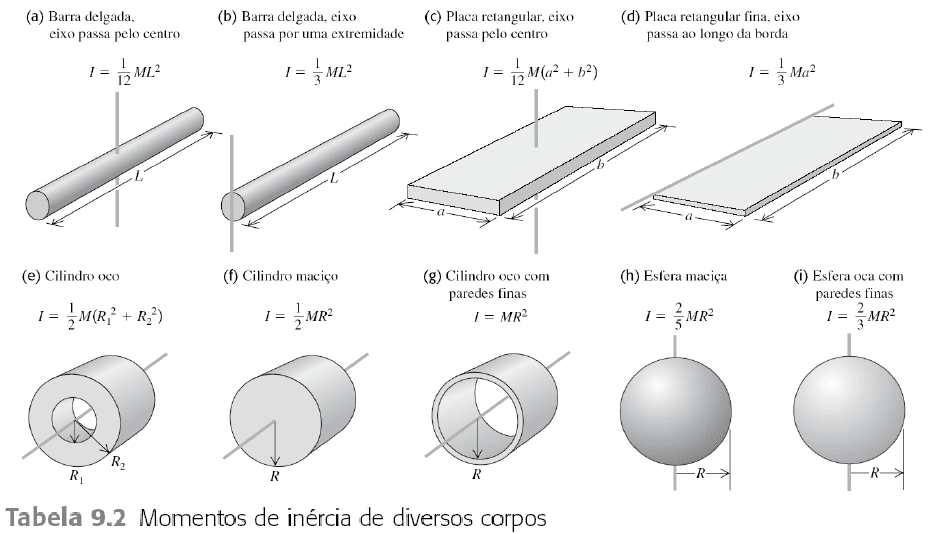
Onde I é o momento de inércia (em kg\cdot m^{2}) e \vec{\omega} é a velocidade angular. Esta fórmula mostra que quanto mais rápido o corpo girar, maior será o momento angular. Momento de inércia é a capacidade de um corpo de resistir à variação da velocidade de rotação. A fórmula para um corpo rígido é:
I=\int r^{2}dm
Onde m é a massa do objeto e r é a distância do eixo de rotação até o limite do corpo rígido. Esta fórmula, com o símbolo \int, é uma integral e a partir dela, dá para encontrar a equação do momento de inércia para qualquer objeto de qualquer forma.
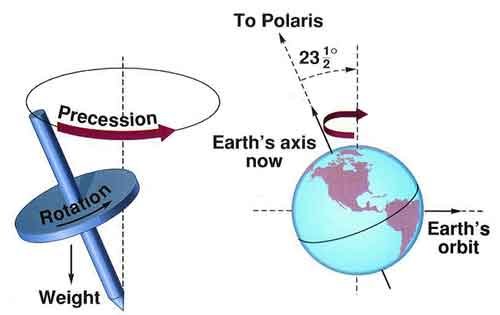
Precessão
A Lei da Conservação do Momento Angular afirma que se o torque resultante for nulo, o momento angular será constante em direção e magnitude. Quanto maior o momento angular, maior a resistência à mudança da direção deste momento, causada por uma força que produz um torque. A força da gravidade causa um torque a 90°, criando um movimento de precessão. Este torque só pode existir com a variação do momento angular em um intervalo de tempo.
\vec{\tau }=\frac{d\vec{L}}{dt}
O d significa variação infinitesimal, uma variação muito pequena que tende a zero, mas não é zero.
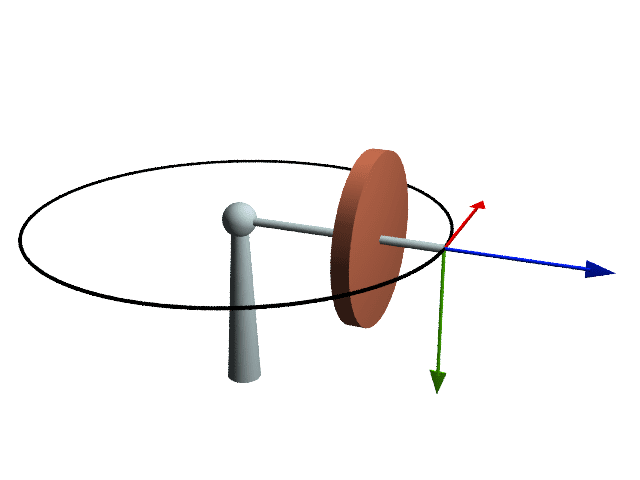
A taxa de precessão (\Omega ) em radianos por segundo (rad/s).
\Omega=\frac{d \theta }{dt}
\theta é o ângulo entre o momento angular L inicial e o momento angular atual L'.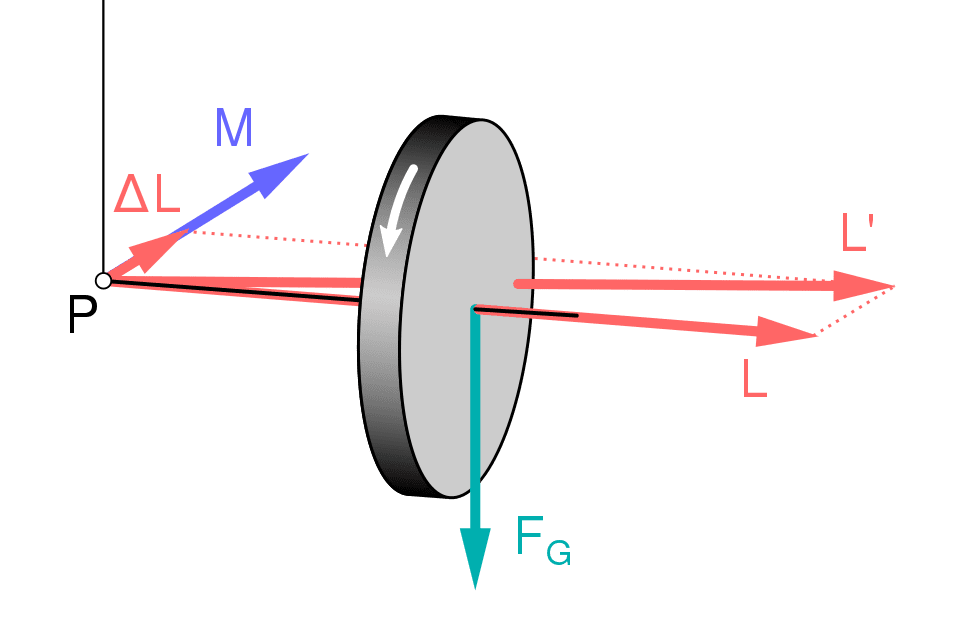
Como \theta é um ângulo infinitesimal ou muito pequeno, pode-se considerar,
\theta \simeq sen\theta=tan \theta =\frac{dL}{L}
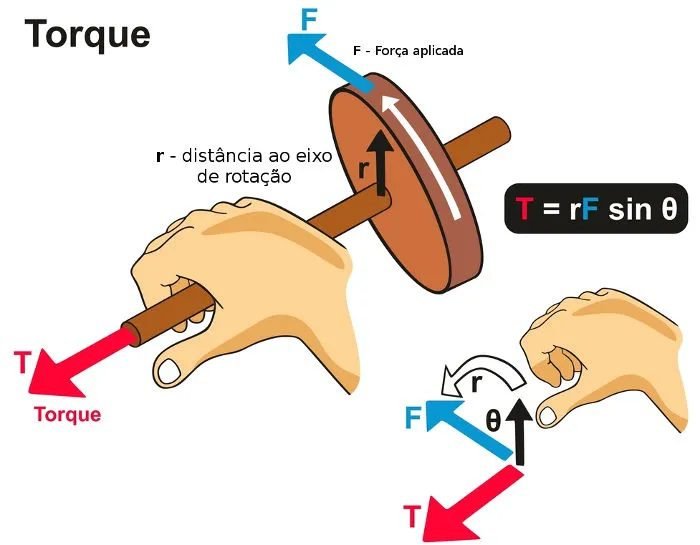
Pois a tangente de um ângulo é o lado oposto dividido pelo adjacente. O torque é a massa M vezes a aceleração da gravidade g vezes o eixo de rotação até o disco r.
dL=\tau dt=(Mgr)dt
d\phi =\frac{dL}{L}=\frac{Mgrdt}{I\omega}
\Omega =\frac{Mgr}{I\omega}
O giroscópio mecânico

Em um giroscópio mecânico, quando a roda central gira em alta velocidade, o eixo central se mantém na mesma direção, não importa os movimentos dos anéis internos e do suporte.
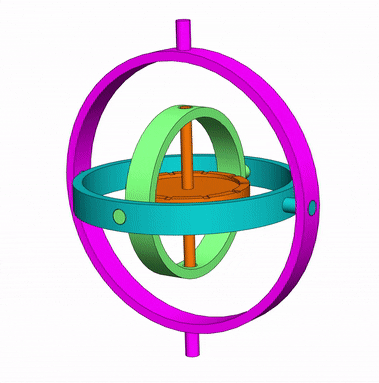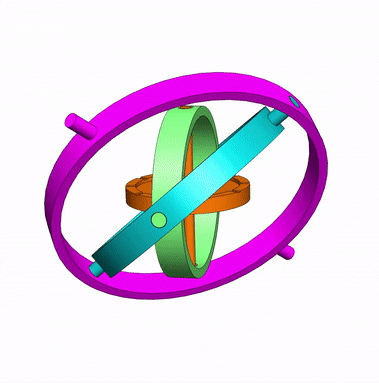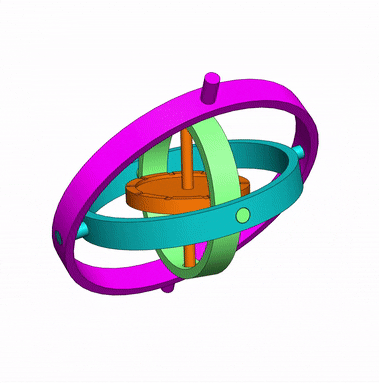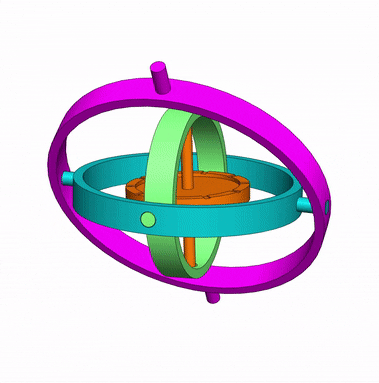
Esta característica é útil para indicar se o avião ou submarino está subindo, descendo ou se mantém na altitude ou profundidade.
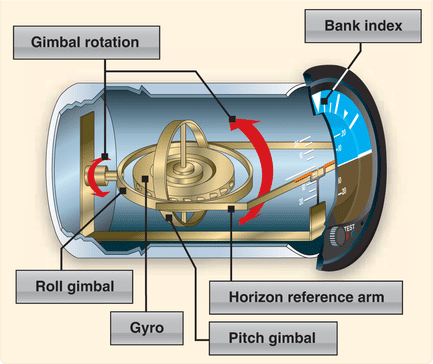

No espaço, onde há poucos pontos de referência, o eixo do giroscópio serve como referência para orientação.
Outros tipos de giroscópios
Giroscópio MEMS
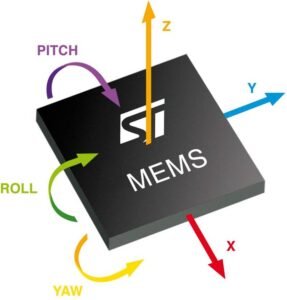
Este é o tipo de giroscópio encontrado em vários sistemas eletrônicos. Consiste em um anel ressonante de silício dentro do chip. Cujo movimentos são convertidos em sinais elétricos muito pequenos que são detectados por eletrodos, mas precisam ser amplificados.
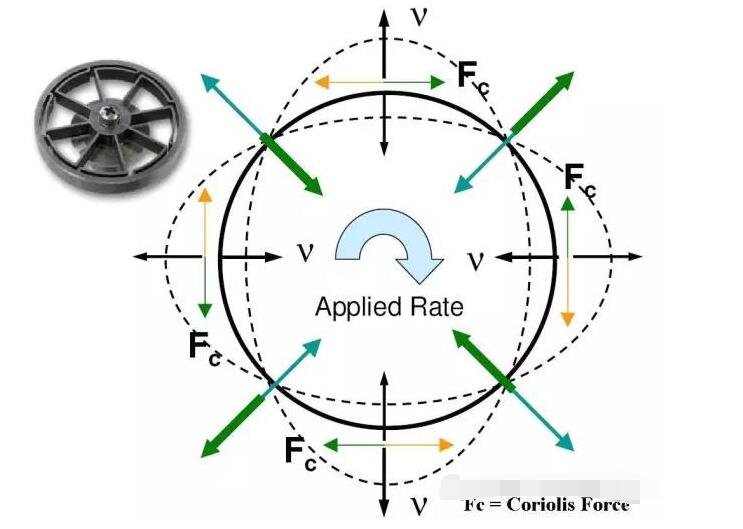
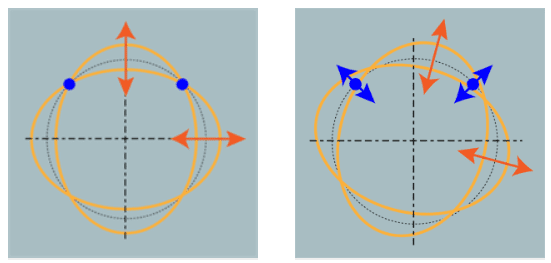
Um vídeo da Silicon Sensing mostra o funcionamento do giroscópio em um veículo.
Existem outros tipos de giroscópios MEMS, com o mesmo princípio de funcionamento, usam uma massa ressonante ligada a molas e com capacitores variáveis para detectar mudanças de capacitância quando a massa recebe uma aceleração angular.

Giroscópio ótico

Este tipo não precisa de um componente rotativo ou ressonante. Um feixe laser é dividido em dois, que vão para sentidos opostos. Os feixes são refletidos por espelhos e podem se propagar em fibra ótica ou cavidade até chegarem ao sensor ótico. Este tipo usa o efeito Sagnac.
Efeito Sagnac
Quando o dispositivo está parado, os feixes chegam ao mesmo tempo no sensor. Quando o giroscópio ótico rotaciona ou é inclinado, os feixes chegam em tempos diferentes e ficam com diferença de fase entre si. Consequentemente, o padrão de interferência entre os feixes muda. Girar em sentidos opostos produz padrões diferentes. Um vídeo da universidade EPFL, na Suiça, mostra o efeito Sagnac.



