This post’s subject is the gyroscope. An instrument of great utility for electronic devices and for air, naval, and space navigations.
Operation principle
Angular momentum

Every rotating object has an angular momentum parallel to the rotation axis.
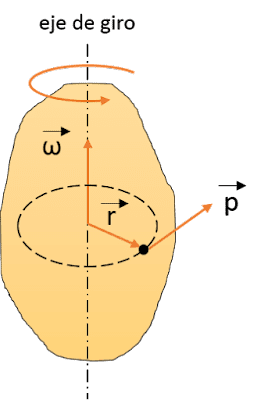
The formula to calculate the angular momentum vector, in kg\cdot m^{2}/s.
\vec{L}=I\cdot \vec{\omega}
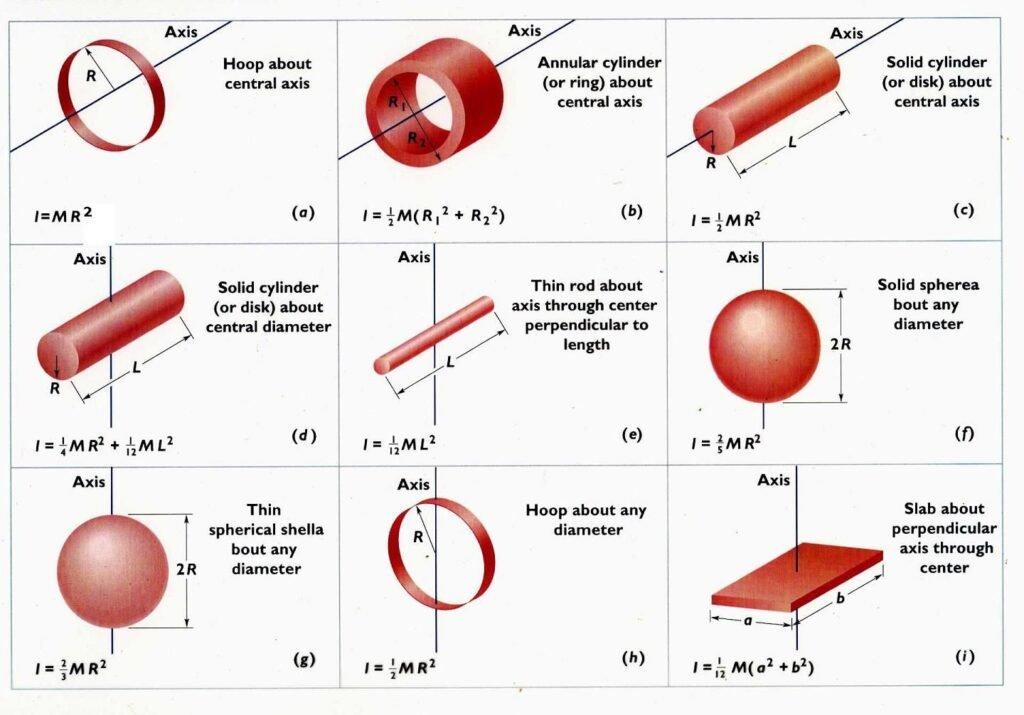
Where I is the moment of inertia (in kg\cdot m^{2}) and \vec{\omega} is the angular speed. This formula shows that faster the body spins, higher will be the angular momentum. Moment of inertia is the capacity of a body to resist the variation of speed rotation. The formula for a rigid body is:
I=\int r^{2}dm
Where m is the object’s mass and r is the distance from rotation axis to the rigid body’s edge. This formula, with the symbol \int, is an integer and from it, you can find the equation of moment of inertia to any object of any shape.
Precession
The Law of Angular Momentum Conservation claims that if the resulting torque is null, the angular momentum will be constant in direction and magnitude. When higher the angular momentum, higher the resistance to change of this momentum’s direction, caused by a force that produces a torque. The gravity force causes a torque at 90°, creating the precession motion. This torque can only exist with the variation of angular momentum in a time interval.
\vec{\tau }=\frac{d\vec{L}}{dt}
The d means infinitesimal variation, a variation so low that tends to zero, but it isn’t zero.
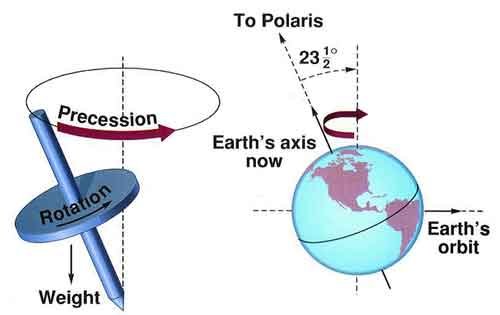
The precession rate (\Omega ) in radians per second (rad/s).
\Omega=\frac{d \theta }{dt}
\theta is the angle between the initial angular momentum L and the current angular momentum L'.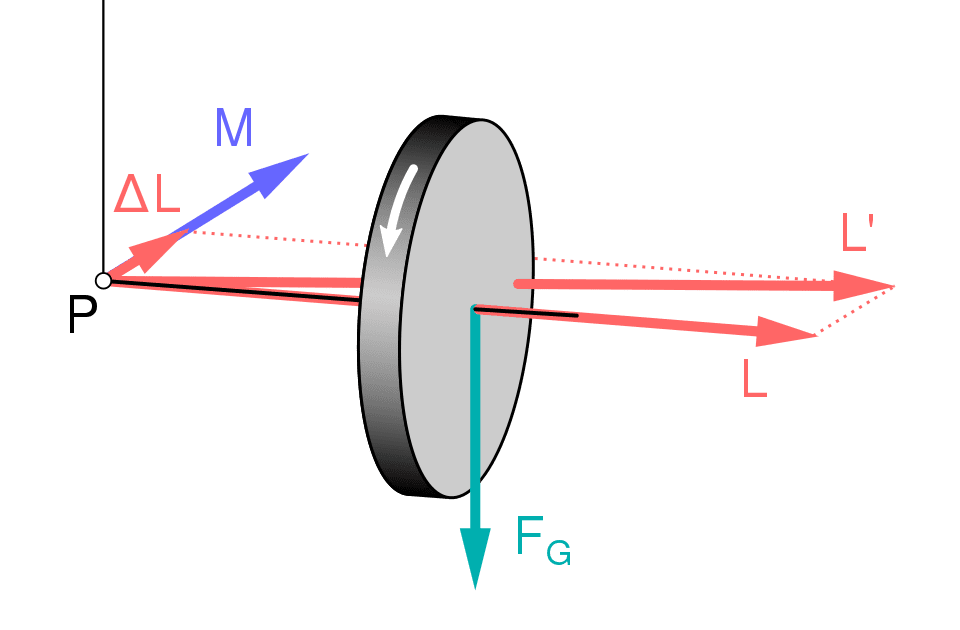
Since \theta is an infinitesimal angle or very small, you can consider,
\theta \simeq sen\theta=tan \theta =\frac{dL}{L}
Because an angle’s tangent is the opposite side divided by adjacent. The torque is the mass M times gravity acceleration g times rotation axis to the disk r.
dL=\tau dt=(Mgr)dt
d\phi =\frac{dL}{L}=\frac{Mgrdt}{I\omega}
\Omega =\frac{Mgr}{I\omega}
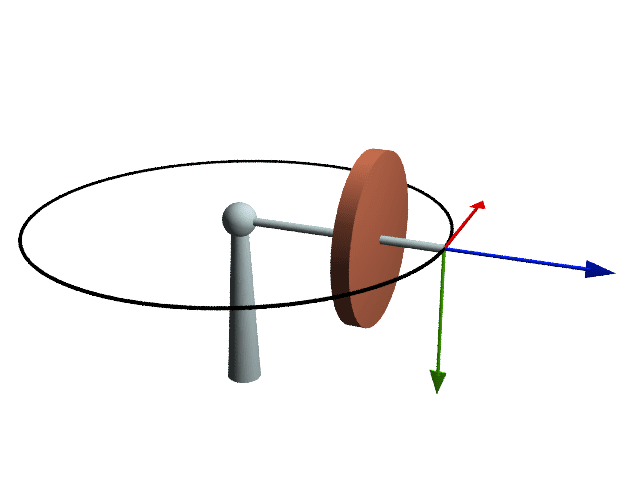
The mechanical gyroscope

In a mechanical gyroscope, when the central wheel spins at a high speed, the central axis will keep in the same direction, doesn’t matter the motion of inner rings and support.
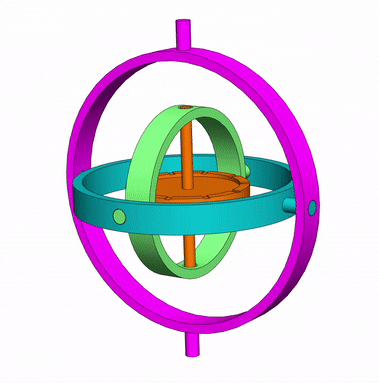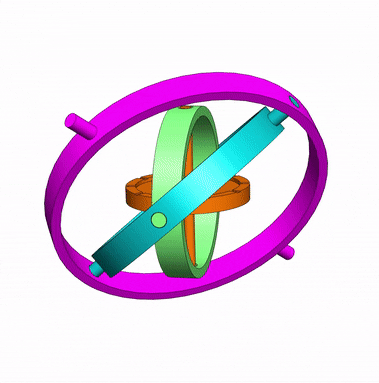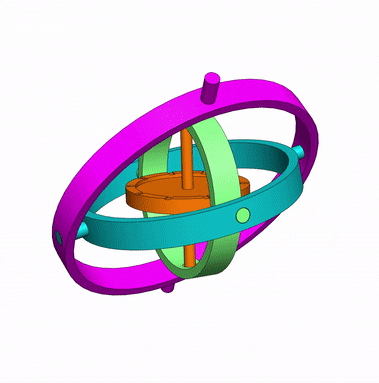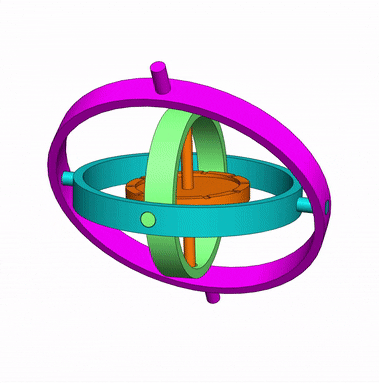
This feature is useful to indicate if the aircraft or submarine is going up, down, or is kept at the same altitude or depth.
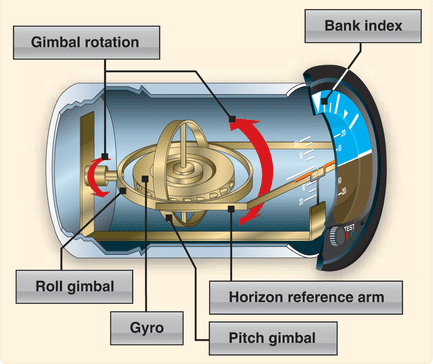

In space, where there are few reference points, the gyroscope’s axis serves as a reference for orientation.
Other types of gyroscopes
MEMS gyroscope
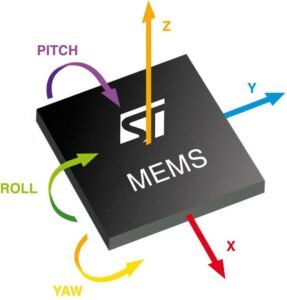
This is the type of gyroscope found in many electronic systems. Consist of a resonant silicon ring inside the chip. Whose movements are converted into very small electric signals that are detected by electrodes, but need to be amplified.

A Silicon Sensing video shows the operation of the gyroscope inside a vehicle.
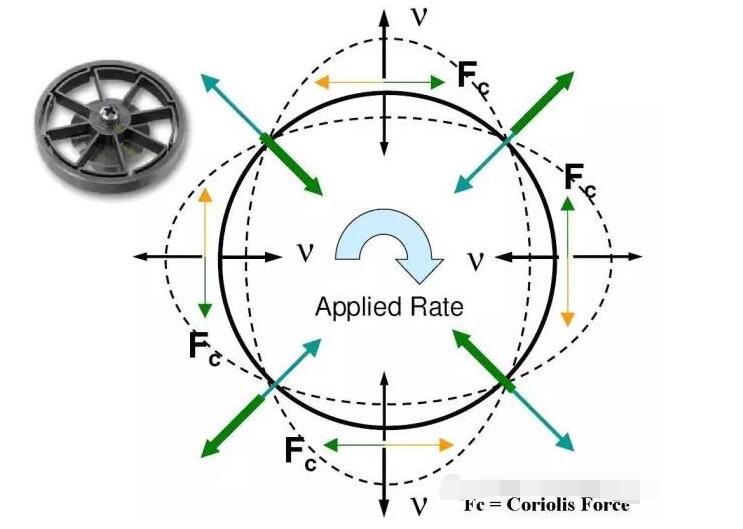
Exist other types of MEMS gyroscopes, with the same operation principle, use a resonant mass linked to springs and with variable capacitors to detect changes in capacitances when the mass receives angular acceleration.

Optical gyroscope

This type doesn’t need a rotative or resonant component. A laser beam is split in two, that go in opposite directions. The beams are reflected by mirrors and can propagate in optical fiber or cavity until arrive at an optical sensor. This type uses the Sagnac effect.
Sagnac effect
When the device is stopped, the beams arrive at the same time on the sensor. When the optical gyroscope is rotated or tilted, the beams arrive at different times and have a phase difference from each other. Consequently, the interference pattern between the beams changes. Spin in opposite directions produces different patterns. A video from EPFL university, in Switzerland, shows the Sagnac effect.



