PID controller tuning: Ziegler-Nichols methods

The classical Ziegler-Nichols methods, introduced in 1942, are some of the most known and applied tuning methods for PID controllers.

In case you don’t know what is PID, I recommend to read the post about the subject before continue.

Link to post about PIDClick here

Ziegler-Nichols for step response

Ziegler-Nichols methods were develop empirically, with observation and practice in many different plants. The plant is considered a black box, don’t need to know it’s equations. But, must know the transient response curve in output when there is set point change.

Was shown in post about PID, outputs of proportional, integral and derivative in time domain. Converting to s domain, these output are as shown below.

Equation and diagram of PID controller in series, on s domain, respectively:

G_{c}(s)=Kp[1+\frac{1}{sT_{i}}]\cdot [1+sT_{d}]=[Kp+\frac{Ki}{s}]\cdot [Kp+sKd]

Equation and diagram of PID parallel controller:

G_{c}(s)=Kp[1+\frac{1}{sT_{i}}+sT_{d}]=Kp+\frac{Ki}{s}+sKd

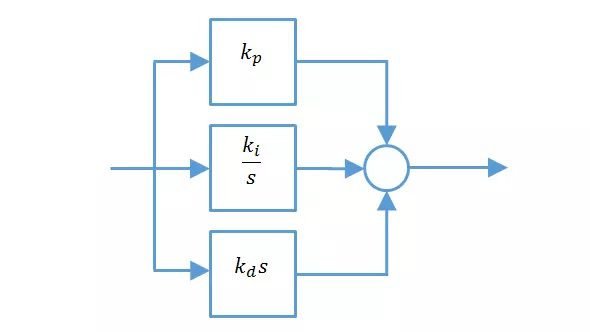
Integral Ki and derivative Kd gains are:

Ki=\frac{Kp}{Ti}

Kd=Kp\cdot Td

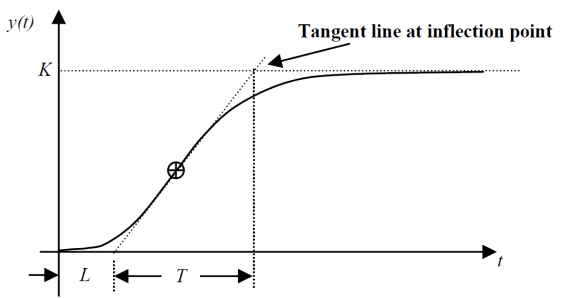
Ziegler-Nichols methods are a set of equations to calculate values of proportional gain Kp, integral time T_{i} and derivative time T_{d}. Considerate response curve showed below.

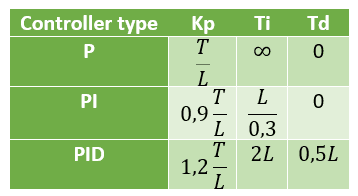
This is the equation set to obtain Kp, T_{i} and T_{d}.

This method can be used in open loop processes, by that, without feedback. Parameters tuning with this method is only applicable if process response to step signal is a curve which reminds a “S”, as shown above.

Critical gain for oscillation method

This is Ziegler-Nichols second method, must determine system’s critical gain to output have a stable oscillatory response. Can only be applied in closed loop systems, because feedback is a prerequisite to create oscillations.

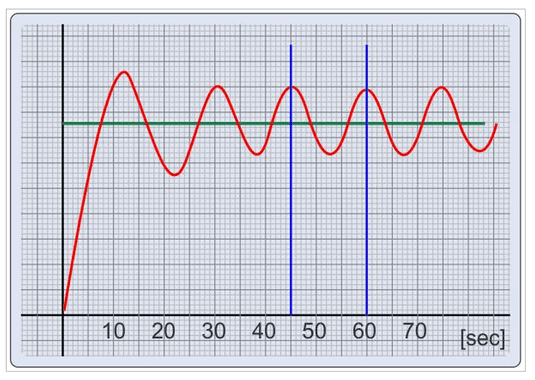
How to find out the critical gain K_{CR}? I and D blocks must be off and proportional gain must be increased until obtain oscillation in output. Obviously, it is made with simulators to avoid damages to physical processes. Other alternative is use computational tools as rlocus from MATLAB. After find K_{CR}, must apply equation set shown in table below to calculate parameters. P_{CR} is critical period of output wave.

With both methods, can obtain an overshoot in maximum 25% of set point value. Can bring goods result of stability and speed to majority of systems.