The skin effect appears in transmission lines that transport alternate current. This effect’s cause is explained in this post.
The phenomenon
In continuous current, electrons distribute and move uniformly in a conductor section. However, with an alternate current, a variable magnetic field is produced due to constant change of electric charges.
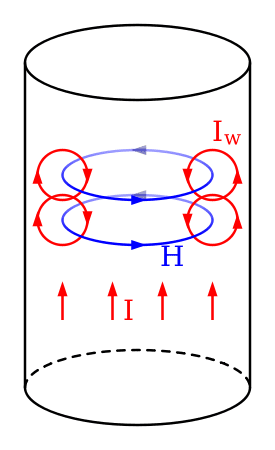
In the center, the currents I and I_{W} have opposite directions and cancel each other. While on periphery, these currents add up. The result is the increase of current density on wire’s periphery and reduction close to the center. When higher the frequency, higher the skin effect.

It’s because of that you can’t use solid wires to transmit AC signal at high frequency. In these situations, are used hollow conductors, saving weight and cost with materials.



AC resistance
Due to skin effect, must be considered two types of resistance: DC and AC. The relation between the resistances is given by the equation.
R_{AC}=R_{DC}\cdot k\sqrt{f}
- R_{AC} and R_{DC} are the AC and DC resistances respectively.
- f is the frequency in Hertz (Hz).
- The k depends on the wire’s diameter on American scale AWG.
The penetration depth of skin effect
When the current frequency increases, current density inside the conductor falls exponentially and concentrates on wire’s edges. The skin depth goes from the surface, to where there’s only 37% of density current on surface.
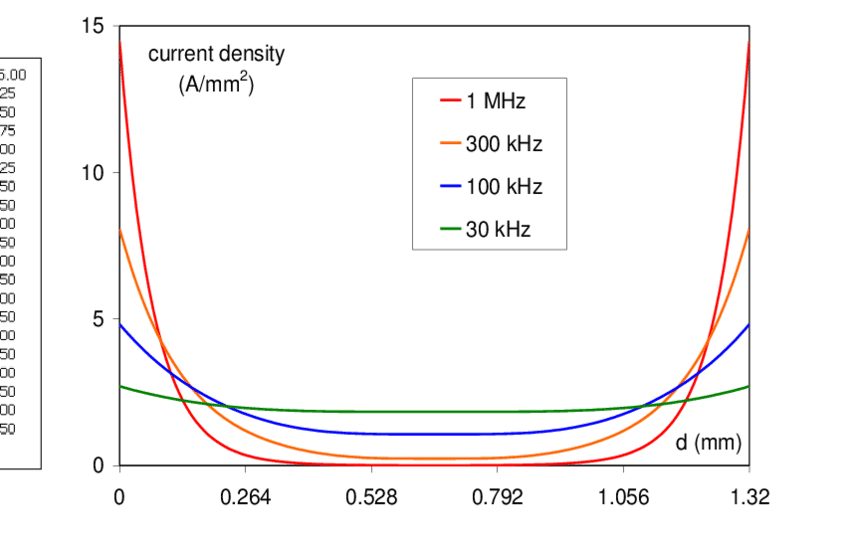
The equation of current density J in a depth.
J=J_{s}e^{\frac{-d}{\delta }}
- J_{s} is the current density on the surface.
- d is the conductor’s diameter.
- \delta is the depth where there is current density. It’s get smaller when increases frequency.
To calculate \delta.
\delta =\sqrt{\frac{2\rho }{\omega \mu }}
- \rho is the electric resistivity on conductor in \Omega \cdot m.
- \omega is the angular frequency in radians per second, can be calculated in the following way.
\omega =2\pi f
- \mu is magnetic permeability in H/m, which is the product of material’s relative permeability \mu _{r} and magnetic permeability in vacuum \mu _{o}, whose value is 1,26\cdot 10^{-6} H/m.
\mu =\mu _{r}\mu _{o}
With manipulations, depth penetration also can be expressed in the following form.
\delta =\sqrt{\frac{1}{\pi f\sigma \mu_{r}\mu _{o}}}
- \sigma is the conductance, the inverse of resistivity.



