This post’s subject is the description of other methods to tune a PID controller. CHR (Chien, Hrone e Reswick) and CC (Cohen e Coon).
In case you don’t know what is PID, access the link below before continuing.
The CHR method
All tuning methods for PID controller consist in calculate values of proportional (K_{p}), derivative (K_{p}) and integral (K_{i}) gains. The CHR method was developed in 1952, as an alternative to solve problems with step response. Despite gains being smaller than the ones obtained by Ziegler-Nichols, the system has more stability when adopts the CHR method.

Defines tuning laws for setpoint change and regulation resistant to disturbances.
Performance criteria
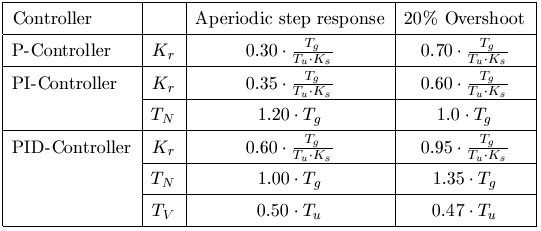
The following tables show gain calculations to obtain the fastest response as possible with 0 or 20% of overshoot for both problems.
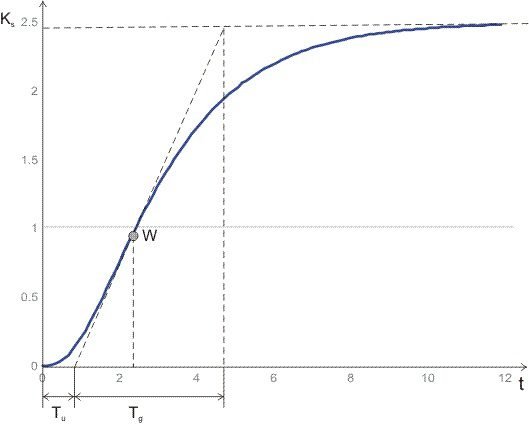
Gain calculation table for problems with regulation with robustness
Ki=\frac{Kp}{T_{N}}
Kd=Kp\cdot T_{V}
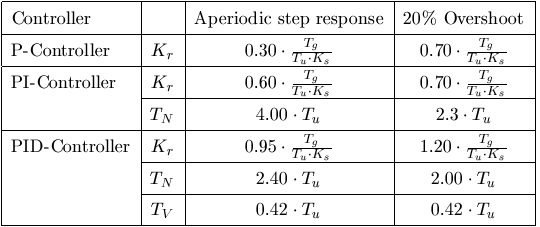
Gain calculation table for servo problem (setpoint change)
Cohen-Coon (CC) method
Developed in 1953, this method is also used for step response and for a system with longer dead time, considering 0,6<\frac{\theta }{\tau }<4,5. However, robustness with be bad if \frac{\theta }{\tau }\leq 2.
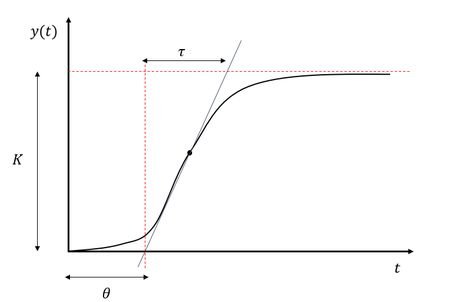
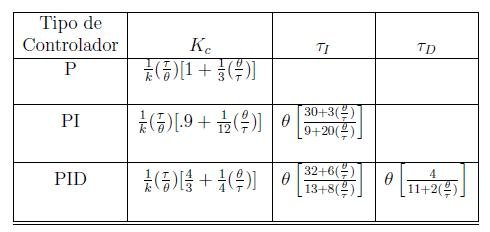
The method Ziegler-Nichols and Cohen-Coon were created to obtain a quarter amplitude damping. In case you want to avoid oscillation, the gain K_{c} must be smaller than the calculated.

In addition to the ones presented today, exist other PID tuning method which will be for future posts.



